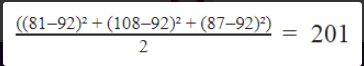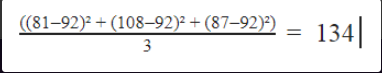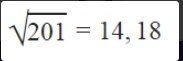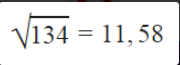Cubo de dados

As aplicações OLAP são usadas pelos gestores em qualquer nível da organização para lhes permitir análises comparativas que facilitem a sua tomada de decisões diárias.
Com ele, o usuário final pode montar diferentes visualizações das informações simplesmente movendo os campos disponíveis entre as áreas do cubo.

Antes de criar em si o cubo OLAP por boa prática vamos criar uma view pois caso a consulta SQL do cubo seja grande, faça a consulta em tabelas referenciando FK, a manutenção do mesmo será fácil.
Exemplo de view: (Oracle, PostgreSQL)

CREATE OR REPLACE VIEW VW_DADOSBPMOFFICE AS
  SELECT cp.idprocesso, 
         cp.status, 
         cpa.descricao AS atividade, 
         pkg_ema.retorna_valor_variavel_texto(cp.idprocesso, 1) AS nomeprocesso, 
         pkg_ema.retorna_valor_variavel_data(cp.idprocesso, 39) AS dataentrega, 
         pkg_ema.retorna_valor_variavel_texto(cp.idprocesso, 16) AS donoproceso, 
         pkg_ema.retorna_valor_variavel_texto(cp.idprocesso, 8) AS solicitante, 
         pkg_ema.retorna_valor_variavel_texto(cp.idprocesso, 4) AS assunto 
  FROM crm_processo cp 
  JOIN crm_processo_atividade cpa ON cpa.idprocesso = cp.idprocesso AND cpa.idatividade = cp.idatividadeatual 
  WHERE cp.idprocedimento = 30 
  AND cpa.idatividade <> 2 
  AND pkg_ema.retorna_valor_variavel_texto(cp.idprocesso, 1) <> '.' 
  AND pkg_ema.retorna_valor_variavel_texto(cp.idprocesso, 16) <> '.'

Assim que criar a view em seu banco de dados vamos ao DOX Estúdio, No modulo Inteligência - > Cubos (OLAP)

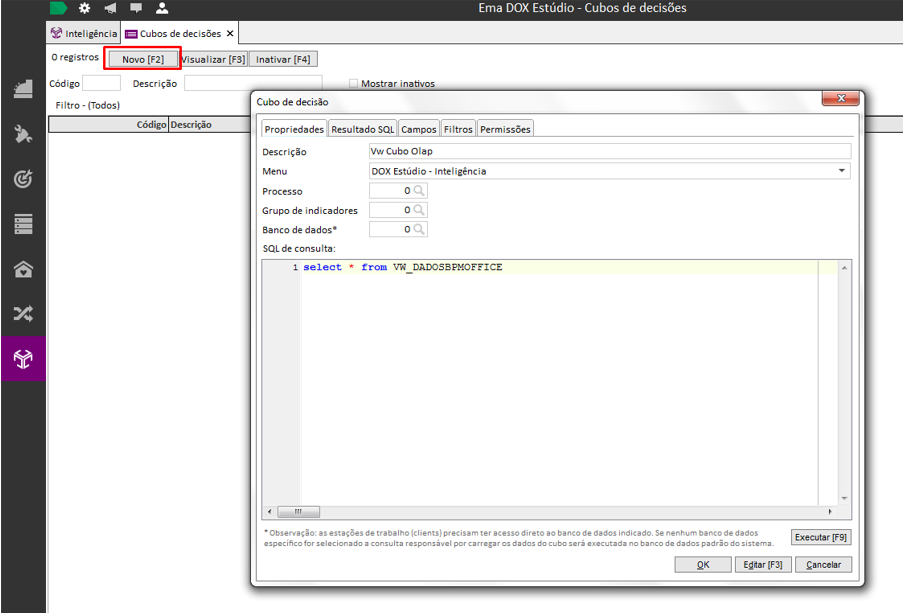
Logo após aperte no botão Novo(F2) e insira as informações necessárias e o SQL da View:

*** Caso o banco de dados não seja informado, o mesmo pegara o banco local em uso.

Configuração de Campos

Um dos principais conceitos de um cubo de dados (OLAP) é que as informações precisam estar distribuídas de forma dinâmica e de fácil manuseamento. Para que um cubo de dados seja montado da melhor forma, é preciso conhecer um pouco mais sobre as áreas de distribuição das informações. Dentre essas áreas, estão:

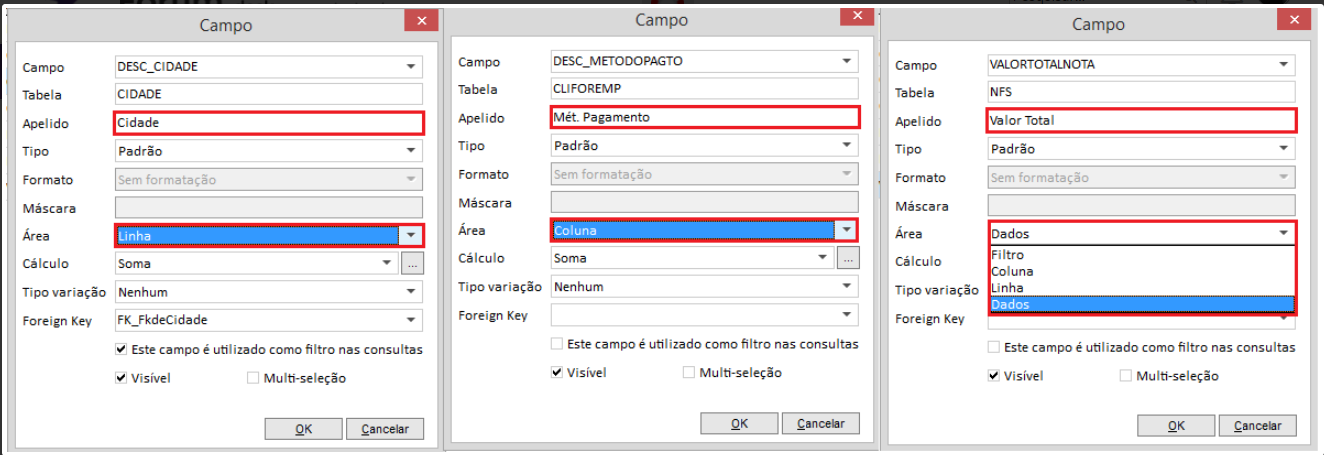
Filtros: são todos os campos configurados pelo usuário que ficam disponíveis para serem exibidos no cubo de dados. Mesmo que não sejam exibidos, esses campos podem ser usados para aplicação de filtros instantâneos sobre os dados apresentados;
Linha: define os campos que servirão como dimensões para os dados apresentados no cubo. Um cubo pode conter vários níveis de dimensões, permitindo realizar o detalhamento gradativo (drill-down) das informações;
Coluna: campos que serão exibidos como colunas no cubo, representando seus grupos de medidas. São muito utilizadas, por exemplo, para representar a variação dos dados ao longo de uma linha de tempo (dias, meses, anos...);
Dados: representam os valores (medidas) das informações apresentadas, sobre os quais podem ser aplicados diferentes tipos de agregações (somas, mínimos, máximos, desvios e variações).

Dentro do Dox, a configuração dos campos com suas respectivas áreas serve para que ao abrir a visualização do Cubo de Dados, os campos venham pré-definidos nas áreas configuradas.

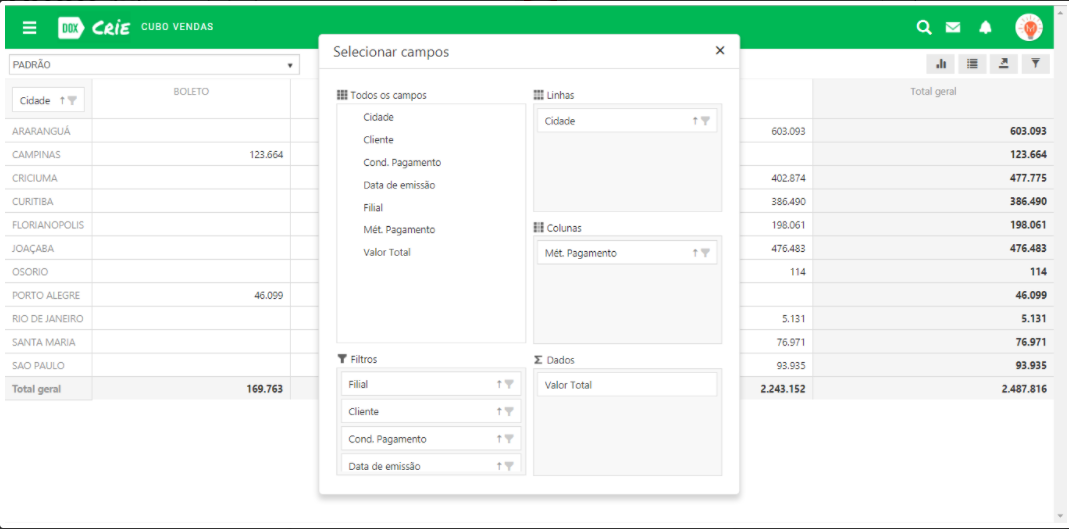
No exemplo, o campo Cidade se encontra como Linha, Mét. de Pagamento como Coluna e Valor Total se encontra como um Dado, portanto, ao visualizar o cubo, é nessa área em que eles se encontrarão, como mostrado na imagem abaixo.

Apesar do criador do Cubo poder definir uma configuração padrão dos campos exibidos em cada área, o usuário final pode montar diferentes visualizações das informações simplesmente movendo os campos disponíveis entre as áreas do cubo.
Esse é o conceito fundamental de um cubo multidimensional: permitir analisar informações sob diferentes ângulos (dimensões), inclusive com diferentes dados e múltiplas formas de agregação.
Para mais informações sobre a configuração de um cubo de dados, você pode assistir à vídeo-aula sobre o assunto clicando aqui.

Agregação de dados

Cada célula na área de dados de um cubo representa o resultado de uma agregação de valores. Esses valores são extraídos de um subconjunto de registros formado pelo cruzamento de cada linha e coluna do cubo.
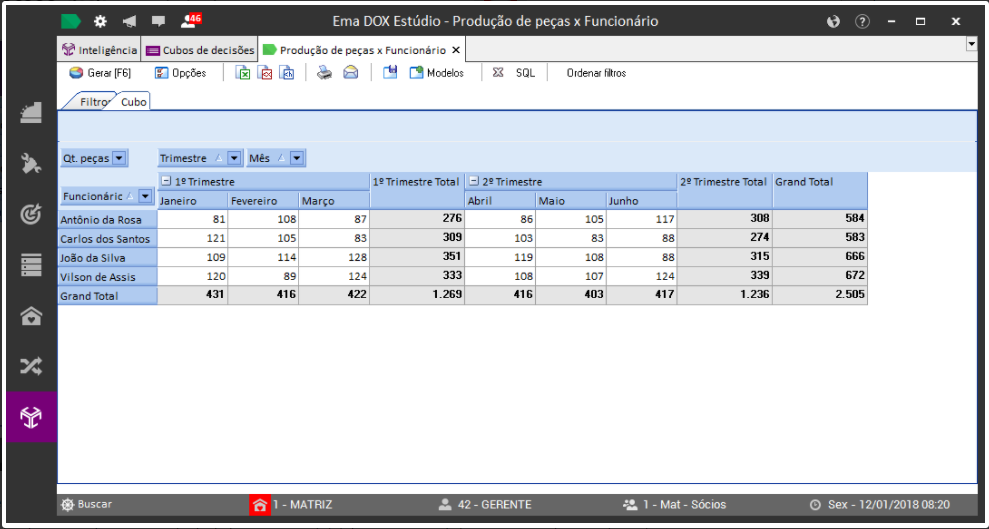
No exemplo abaixo, cada valor representa a quantidade total de peças produzidas por mês de cada funcionário.

Como pode ser observado na figura acima, além do total de peças que cada funcionário produziu em cada mês, o cubo também exibe:

Um totalizador para cada agrupamento de dados: no caso, o total de peças que cada funcionário produziu por trimestre;
Um totalizador geral para cada linha: no caso, o total de peças que cada funcionário produziu ao longo de todo período;
Um totalizador geral para cada coluna de dados: no caso, o total de peças que todos os funcionários produziram em cada mês e em cada trimestre;
Um totalizador geral dos dados do cubo: no caso, o total de 2.505 peças produzidas por todos os funcionários ao longo de todo o período.

Tipos de cálculos

Um cubo de dados permite diversos tipos de cálculo para agregação dos valores disponíveis.
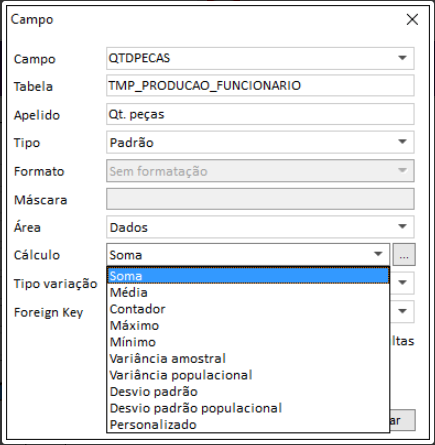
A imagem abaixo apresenta os diferentes tipos de cálculo que podem ser configurados em cada campo de um cubo no Ema DOX

Soma: Realiza a soma dos valores disponíveis em cada cruzamento de linha/coluna. Exemplo: na figura abaixo podemos ver que o funcionário “Antônio da Rosa” produziu a soma total de 276 peças no 1º trimestre (81 em Janeiro + 108 em Fevereiro + 87 em Março, conforme detalhado na imagem "Produção mensal de peças por funcionário").

Média: Calcula a média aritmética dos valores disponíveis em cada cruzamento de linha/coluna. Exemplo: na figura acima podemos ver que o mesmo funcionário “Antônio da Rosa” produziu uma média mensal de 92 peças no 1º trimestre (276 peças/3 meses).

Contador: Apresenta a quantidade de registros englobados em cada cruzamento de linha/coluna. Exemplo: na figura acima podemos ver uma quantidade de 3 registros (Qt. meses) envolvidos na análise.

Máximo: Apresenta o maior valor disponível em cada cruzamento de linha/coluna. Exemplo: na figura acima podemos ver que, no seu mês mais produtivo, o funcionário “Carlos dos Santos” conseguiu fazer 121 peças (no mês de Janeiro, conforme detalhamento na imagem "Produção mensal de peças por funcionário").

Mínimo: Apresenta o menor valor disponível em cada cruzamento de linha/coluna. Exemplo: na Figura x.3 podemos ver que, no seu mês menos produtivo, o funcionário “Vilson de Assis” conseguiu fazer apenas 89 peças (no mês de Fevereiro, conforme detalhamento na imagem "Produção mensal de peças por funcionário").

Variância amostral: Realiza o cálculo da variância (uma medida de dispersão que mostra quão distantes os valores estão da média) com base em uma amostra dos registros observados. O resultado é obtido através da soma dos quadrados da diferença entre cada valor e a média aritmética, dividida pela quantidade de registros observados menos um.

Exemplo: na figura abaixo vemos uma variância amostral de 201 peças para o funcionário “Antônio da Rosa” no 1º trimestre. Considerando que esse funcionário produziu 81 peças em Janeiro, 108 em Fevereiro e 87 em Março, ele teve uma média de 92 peças produzidas por mês no 1º trimestre. Utilizando os dados de produção mensal desse funcionário, o cálculo da variância considerando uma amostra de 2 períodos (3 meses observados menos um) fica assim:

Variância populacional:

Realiza o cálculo da variância com base em todos os registros observados. O resultado é obtido através da soma dos quadrados da diferença entre cada valor e a média aritmética (até aqui, idêntico à variação amostral), só que dividida pela quantidade total de registros observados. Exemplo: na figura acima vemos uma variância populacional de 134 peças para o funcionário “Antônio da Rosa” no 1º trimestre. Utilizando os mesmos dados de produção mensal desse funcionário, o cálculo da variância considerando todos os 3 períodos (meses) fica assim:

Aplicação prática: Observando a figura acima, podemos concluir que a produção mensal do funcionário “João da Silva” é mais uniforme do que a dos demais funcionários (Variância populacional = 150,67). * Quanto maior for a variância, mais distantes da média estarão os valores, e quanto menor for a variância, mais próximos os valores estarão da média.

Desvio padrão: Em certas análises, o cálculo da variância pode não ser suficiente, pois essa é uma medida de dispersão muito influenciada por valores que estão muito distantes da média. Além disso, o fato de a variância ser calculada “ao quadrado” pode causar uma certa camuflagem dos valores, dificultando sua interpretação. Uma alternativa para solucionar esse problema a aplicação de uma outra medida de dispersão: o desvio padrão. Na prática, o desvio padrão indica qual é o “erro” se quiséssemos substituir um dos valores coletados pelo valor da média. Para calcular o desvio padrão, basta obter o resultado positivo da raiz quadrada da variância amostral. Exemplo: na figura abaixo vemos um desvio padrão de 14,18 peças para o funcionário “Antônio da Rosa” no 1º trimestre. Considerando a variância amostral desse funcionário no mesmo período (201), o cálculo do desvio padrão fica simples, assim:

Desvio padrão populacional: O desvio padrão populacional segue o conceito do desvio padrão, com a diferença de que é calculado com base na variância populacional. Exemplo: na figura acima vemos um desvio padrão populacional de 11,58 peças para o funcionário “Antônio da Rosa” no 1º trimestre. Considerando a variância populacional desse funcionário no mesmo período (134), o cálculo fica assim:

Personalizado: Além dos cálculos automáticos descritos anteriormente, o Ema DOX permite montar seu próprio cálculo personalizado para cada campo disponível no cubo de dados. Abrindo o assistente para elaboração do cálculo personalizado (figura acima), é possível montar uma expressão que retorne o resultado desejado para o campo em questão, utilizando:

Valores fixos: 0, 0.5, 100, 200, 5000, etc.
Valores dos outros campos configurados no cubo: /*QTDPECAS*/, /*QTDMESES*/, /*MES*/, /*TRIMESTRE*/, etc.
Expressões condicionais: seguindo o formato “Se ? Entao ? Senao”;
Operadores matemáticos básicos: adição (+), subtração (-), multiplicação (*), divisão (/));
Operadores comparativos: igual (=), diferente (<>), menor (<), maior(>).

Exemplo: na figura abaixo, vemos que o funcionário “Carlos dos Santos” produziu uma média de 5,5 peças por dia durante o mês de janeiro. Esse valor foi obtido através de um cálculo personalizado, dividindo o total de peças produzidas no mês (121) pela quantidade de dias trabalhados (22).

Variações dos cálculos

Além de poder configurar diferentes tipos de cálculo empregados sobre os dados de um cubo, é possível definir uma variação a ser aplicada sobre cada cálculo realizado. O Ema DOX contempla os seguintes tipos de variações de cálculos:

Nenhum: Não aplica qualquer variação sobre o cálculo realizado, mantendo seu valor original.

Absoluto: Apresenta a diferença absoluta entre o valor calculado da célula atual e o valor calculado para o mesmo campo na coluna imediatamente anterior. Na figura abaixo, Tipos de variações, vemos que o funcionário “Antônio da Rosa” produziu 32 peças a mais no 2º trimestre em comparação com o total de peças produzido no período anterior (1º trimestre). Essa diferença foi obtida da seguinte forma: Calculando a quantidade total de peças produzidas no segundo período (308); Pegando a quantidade total de peças produzidas já calculada no primeiro período (276); Subtraindo o total obtido no 1º período do total obtido no 2º período. Seguindo essa lógica, o cálculo da variação absoluta fica assim: 308 - 276 = 32

Percentual: Apresenta a diferença percentual entre o valor calculado da célula atual e o valor calculado para o mesmo campo na coluna imediatamente anterior. Na figura abaixo, Tipos de variações, vemos que o funcionário “João da Silva” teve uma queda de produtividade de 10,26% no 2º trimestre em comparação com o total de peças produzido no período anterior (1º trimestre). Essa diferença foi obtida com o seguinte cálculo: ((315 – 351) / 351) * 100 = -10,26

Percentual da coluna: Calcula o percentual que o valor da célula atual representa em relação ao valor total da coluna. Na figura abaixo, Tipos de variações, vemos que a produção do funcionário “Vilson de Assis” no 1º trimestre (333 peças) corresponde a 26,24% da produção somada de todos os funcionários nesse período (1.269 peças). Sendo assim, o cálculo empregado foi o seguinte: (333 / 1269) * 100 = 26,24

Percentual da linha: Calcula o percentual que o valor da célula atual representa em relação ao valor total da linha. Na figura abaixo, Tipos de variações, vemos que a produção total do funcionário “Vilson de Assis” no período analisado (672 peças) corresponde a 26,83% da produção somada de todos os funcionários no período (2.505 peças). Sendo assim, o cálculo empregado foi o seguinte: (672 / 2505) * 100 = 26,83